알고리즘, Sort, Bubble Sort

버블 정렬(Bubble Sort)은 간단한 정렬 알고리즘 중 하나로, 인접한 두 요소를 비교하여 필요에 따라 위치를 바꾸면서 리스트를 정렬하는 방식입니다. 버블 정렬의 이름은 가장 큰 요소가 반복적으로 리스트의 끝으로 "부풀어 오르는" 과정에서 유래되었습니다.

기본 개념

버블 정렬의 기본 개념은 다음과 같습니다:

1. 비교 및 교환: 리스트의 처음부터 시작하여 인접한 두 요소를 비교합니다. 만약 첫 번째 요소가 두 번째 요소보다 크면 두 요소의 위치를 바꿉니다.
2. 반복: 리스트 끝까지 이 과정을 반복합니다. 이 과정을 반복하면 가장 큰 요소가 리스트의 끝으로 이동합니다.
3. 반복 감소: 리스트 끝에 가장 큰 요소가 고정되면 다음 반복에서는 마지막 요소를 제외한 나머지 요소를 비교합니다.
4. 정렬 완료: 더 이상 교환이 필요하지 않을 때까지 이 과정을 반복합니다.

예제

다음은 자바스크립트로 구현한 버블 정렬의 예제입니다.

function bubbleSort(arr) {
  let swaps = true;
  for (let i = arr.length; i > 0; i--) {
    for (let j = 0; j < i - 1; j++) {
      if (arr[j] > arr[j + 1]) {
        let temp = arr[j];
        arr[j] = arr[j + 1];
        arr[j + 1] = temp;
        swaps = false;
      }
    }
    if (swaps) break;
  }
  return arr;
}

console.log(bubbleSort([1, 6, 3, 10, 2, 15]));

// [ 1, 6, 3, 10, 2, 15 ]
// [ 1, 3, 6, 10, 2, 15 ]
// [ 1, 3, 6, 2, 10, 15 ]
// [ 1, 3, 2, 6, 10, 15 ]
// [ 1, 2, 3, 6, 10, 15 ]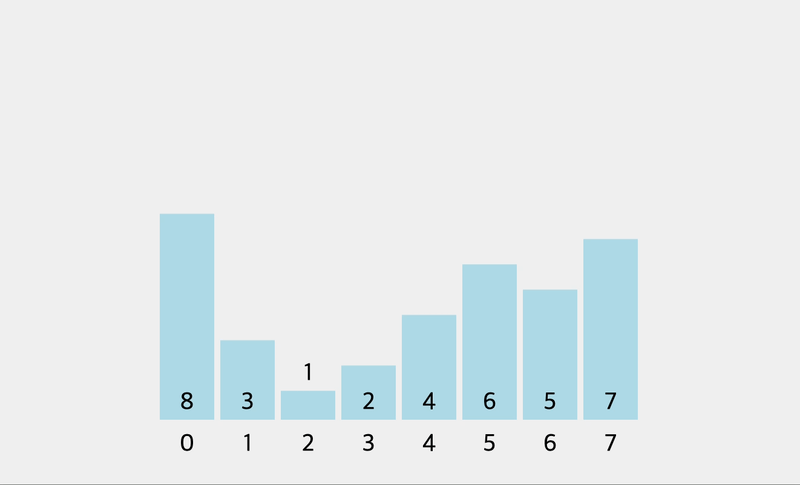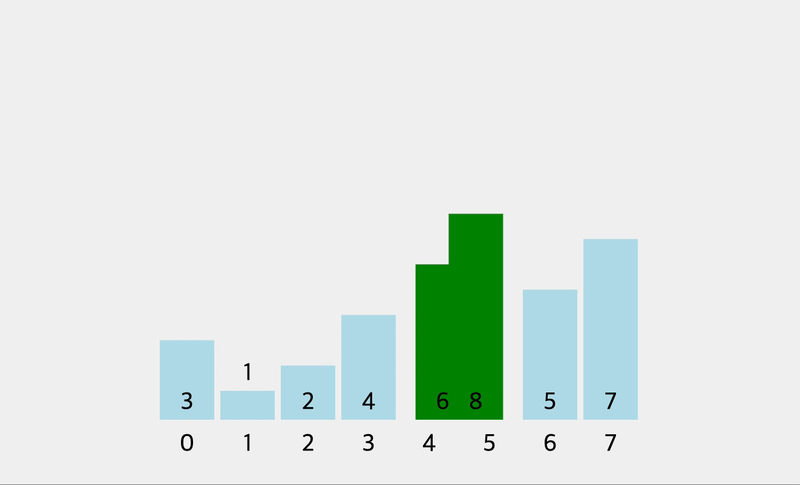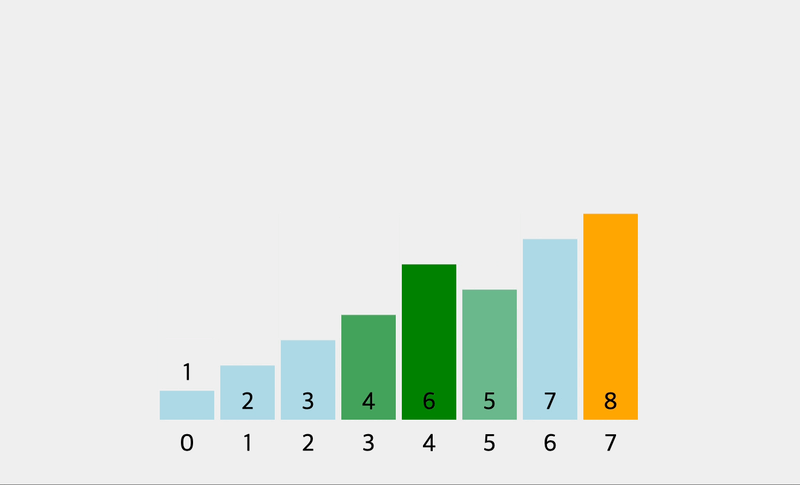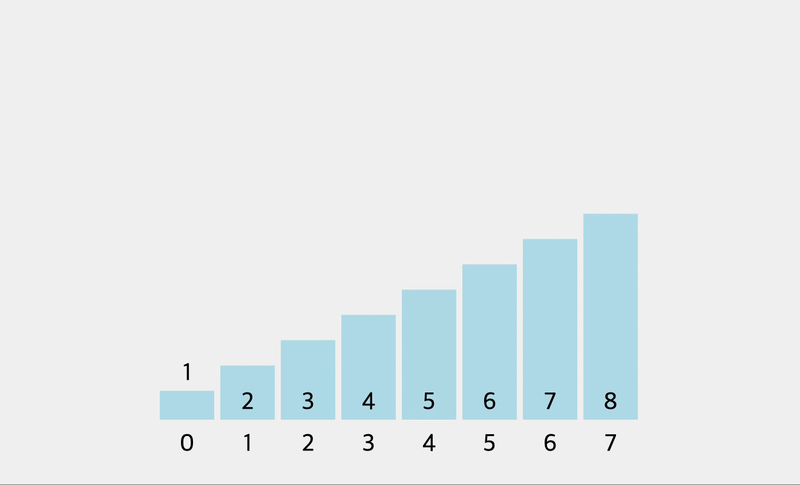

 

시간 복잡도

버블 정렬의 시간 복잡도는 다음과 같습니다:

• 최악의 경우 시간 복잡도: O(n^2)
  • 리스트가 역순으로 정렬된 경우 모든 요소를 비교하고 교환해야 합니다.
• 평균 시간 복잡도: O(n^2)
• 최선의 경우 시간 복잡도: O(n)
  • 리스트가 이미 정렬된 경우 한 번의 반복만으로 정렬이 완료됩니다.

특징

1. 단순함: 버블 정렬은 구현이 매우 간단합니다.
2. 안정성: 동일한 값의 요소들이 입력 순서를 유지합니다.
3. 비효율성: 시간 복잡도가 O(n^2)로, 큰 리스트에 대해서는 비효율적입니다. 이는 실제로 사용되는 경우가 드문 이유입니다.

최적화

버블 정렬은 이미 정렬된 경우 비교를 최소화하기 위해 최적화할 수 있습니다. 만약 어떤 반복에서 교환이 발생하지 않으면 리스트가 이미 정렬된 것이므로 정렬을 종료할 수 있습니다.

function optimizedBubbleSort(arr) {
    let n = arr.length;
    let swapped;

    do {
        swapped = false;
        for (let i = 0; i < n - 1; i++) {
            if (arr[i] > arr[i + 1]) {
                let temp = arr[i];
                arr[i] = arr[i + 1];
                arr[i + 1] = temp;
                swapped = true;
            }
        }
        n--;
    } while (swapped);

    return arr;
}

let arr = [3, 2, 1, 4, 5];
console.log(optimizedBubbleSort(arr)); // [1, 2, 3, 4, 5]

이 최적화는 최선의 경우 시간 복잡도를 O(n)으로 줄여줍니다.

결론

버블 정렬은 이해하고 구현하기 쉬운 정렬 알고리즘으로 교육용으로 자주 사용됩니다. 하지만 시간 복잡도 측면에서 비효율적이기 때문에 실제로는 크기가 작은 배열을 제외하고는 잘 사용되지 않습니다. 대부분의 경우, 퀵 정렬(Quick Sort), 병합 정렬(Merge Sort), 힙 정렬(Heap Sort)과 같은 더 효율적인 정렬 알고리즘을 사용하는 것이 좋습니다.