알고리즘, Sort, Quick Sort

퀵 정렬(Quick Sort)은 Divide and Conquer 기법을 사용하는 매우 효율적인 정렬 알고리즘입니다. 평균적으로 매우 빠른 시간 복잡도인 O(n log n)을 가지며, 제자리 정렬(In-place Sort) 알고리즘입니다. 퀵 정렬은 리스트에서 피벗(pivot) 요소를 선택하고, 이를 기준으로 리스트를 두 개의 하위 리스트로 나누는 과정을 반복하여 정렬합니다.

기본 개념

퀵 정렬의 기본 개념은 다음과 같습니다:

1. 피벗 선택: 리스트에서 피벗 요소를 선택합니다.
2. 분할: 피벗을 기준으로 리스트를 두 개의 하위 리스트로 분할합니다. 피벗보다 작은 요소들은 피벗의 왼쪽으로, 피벗보다 큰 요소들은 피벗의 오른쪽으로 이동합니다.
3. 재귀 호출: 분할된 하위 리스트에 대해 퀵 정렬을 재귀적으로 호출합니다.
4. 결합: 하위 리스트가 정렬되면 이들을 결합하여 전체 리스트를 정렬합니다.

예제

다음은 자바스크립트로 구현한 퀵 정렬의 예제입니다.

function swap(arr, idx1, idx2) {
  let temp = arr[idx1];
  arr[idx1] = arr[idx2];
  arr[idx2] = temp;
}

function pivot(arr, start = 0, end = arr.length + 1) {
  var pivot = arr[start];
  var swapIdx = start;

  for (var i = start + 1; i < arr.length; i++) {
    if (pivot > arr[i]) {
      swapIdx++;
      swap(arr, swapIdx, i);
    }
  }
  swap(arr, start, swapIdx);
  return swapIdx;
}

console.log(pivot([5, 2, 1, 8, 4, 7, 6, 3])); // 3

function quickSort(arr, left = 0, right = arr.length - 1) {
  if (left < right) {
    let pivotIndex = pivot(arr, left, right);

    // left
    quickSort(arr, left, pivotIndex - 1);
    // right
    quickSort(arr, pivotIndex + 1, right);
  }
  return arr;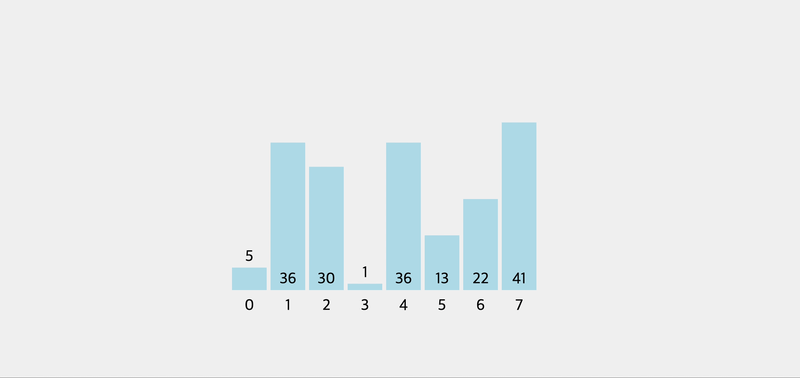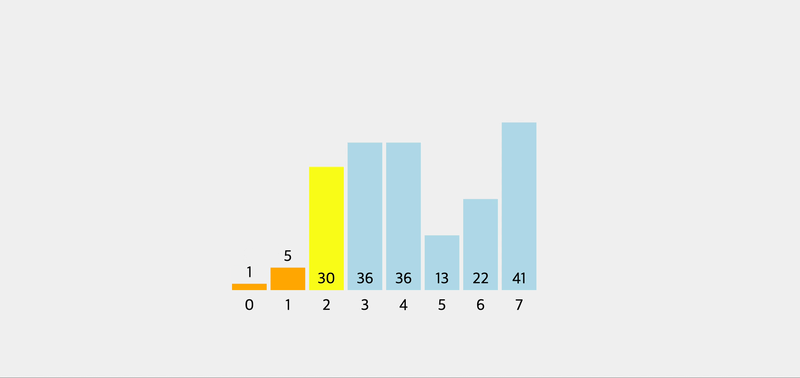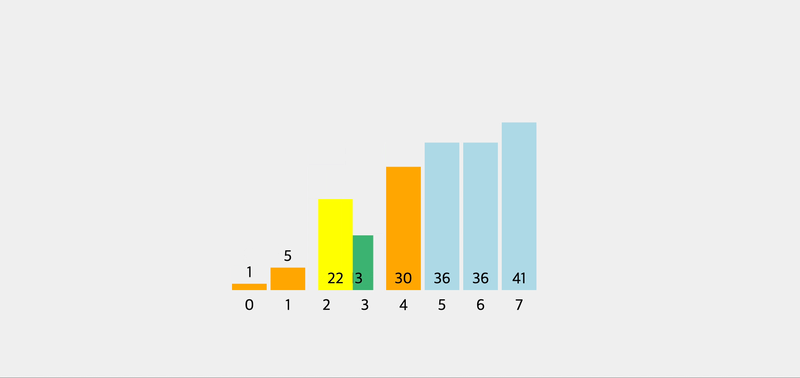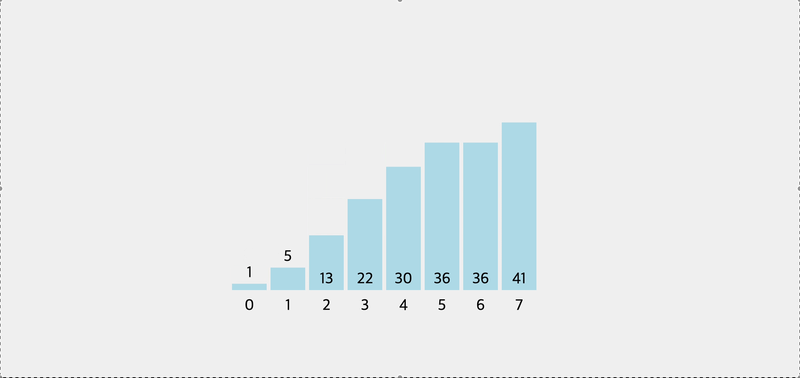
}

 

시간 복잡도

퀵 정렬의 시간 복잡도는 다음과 같습니다:

• 최악의 경우 시간 복잡도: O(n^2)
  • 리스트가 이미 정렬된 경우나 피벗이 최솟값이나 최댓값으로 선택되는 경우입니다.
• 평균 시간 복잡도: O(n log n)
  • 리스트가 균등하게 분할되는 경우입니다.
• 최선의 경우 시간 복잡도: O(n log n)
  • 피벗이 항상 리스트의 중앙값을 선택하여 균등하게 분할되는 경우입니다.

특징

1. 제자리 정렬(In-place Sort): 퀵 정렬은 추가적인 메모리 공간을 거의 사용하지 않습니다.
2. 비교 기반 정렬(Comparison Sort): 요소들을 비교하여 정렬합니다.
3. 불안정 정렬(Unstable Sort): 동일한 값의 요소들이 입력 순서를 유지하지 않을 수 있습니다.

결론

퀵 정렬은 평균적으로 매우 빠른 정렬 알고리즘으로, 대부분의 실용적인 정렬 작업에 사용될 수 있습니다. 제자리 정렬이 가능하고, 추가 메모리 사용이 적어 효율적입니다. 그러나 최악의 경우 시간 복잡도가 O(n^2)일 수 있으므로, 피벗 선택 최적화와 같은 다양한 최적화 기법을 사용하여 성능을 향상시킬 수 있습니다.